|
|
|
|
|
|
|
|
| Lecturer: | Prof. Dr. Ernst W. Mayr |
| Time: |
lecture Monday 14:15-16:00, 4 hours solving of programming assignments (6 SWS) |
| Room: | Lecture Hall S2229, Programming exercises can be solved in computer room S2237 |
| Area: |
Computer Science I (old regulations) Computer Science III (new regulations) (Details here) |
| Prerequisites: | Vordiplom; courses Effiziente Algorithmen I and II recommended |
| Coordinator: | Thomas Erlebach, Thomas Schickinger |
| Registration: | the centralized registration takes place at the HP-Halle |
| Certificate: | solving all programming exercises (students work in groups of two) and passing a final oral exam |
For many problems that are encountered in practice can be solved efficiently if they are modeled as graph problems. For several decades researchers in mathematics and computer science have devised algorithms for the efficient solution of typical graph problems. It has been shown that many problems can be solved by very fast algorithms even though a straightforward implementation requires exponential running-times.
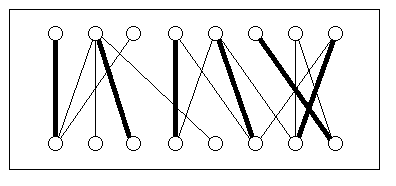
So-called matching algorithms, for example, can be used to solve a variety of assignment problems. One such problem could be to assign lecturers to courses in a way that ensures that the maximum possible number of courses can be taught. If every lecturer teaches at most one course and every course is taught at most once, the problem is equivalent to the matching problem in a bipartite graph as depicted in the figure above. The top row of nodes represents lecturers, the bottom row represents courses. An edge between a lecturer node and a course node means that the lecturer is competent to teach the respective course. Now, a valid assignment of courses to lecturers corresponds to a matching in the graph. In the example above, at most six out of eight courses can be taught. The bold edges correspond to such an assignment. The algorithm by Hopcroft and Karp computes maximum matchings in bipartite graphs in time O(sqrt(n)*m), where n is the number of nodes and m is the number of edges of the graph.
Graph algorithms are interesting not only because of their usefulness for the solution of practical problems, but also because of the algorithmic techniques and the used data structures. Therefore, students who intend to take part in this practical course should be prepared to deal with complicated algorithms.
|
|
depth-first-search, breadth-fist-search |
|
|
connected components |
|
|
minimum spanning trees |
|
|
shortest paths |
|
|
matchings |
|
|
network flow |
|
|
vertex-coloring planar graphs with 5 colors |
|
|
approximating the traveling salesman problem |
In addition to these graph problems, several other problems originating from different application contexts and not directly related to graphs will be covered as well. Examples are:
|
|
string matching |
|
|
computing the edit distance of strings |
Many of these algorithms are presented in the courses "Efficient Algorithms and Data Structures I/II". It is recommended to attend these lectures before taking part in this practical course, but it is not required. A special two-hours-per-week lecture is part of the practical and gives explanations regarding how the algorithms work and how they can be implemented. Proofs of correctness and analyses of running times can not be carried out in full detail most of the time, however. These are presented in the lectures "EA I" and "EA II" instead.
The goal of the practical course is to help students gain a better understanding of how sophisticated algorithms, graph algorithms in particular, work and to convince them of the benefit obtained by using high-level data structures.
LEDA is a class library supplying frequently used data structures such as stacks, queues, priority queues, lists and graphs. Using LEDA reduces substantially the programming effort necessary to implement sophisticated algorithms in C++ efficiently. In addition, the class GraphWin offered by LEDA is a flexible tool for visualization of graph algorithms.
The programming exercises can either be solved in our computer room (S2237), on the workstations in the HP-Halle (beware: compilation of LEDA programs takes quite long here!), or on any PC running Linux (the latter case requires to install LEDA first). Groups of two students solve the programming exercises together. We strongly advise the groups not to divide the work load and work on the exercises separately; instead, they should actually cooperate in solving the problems and implementing the algorithms. In the oral exam at the end of the semester, every student is expected to be knowledgable about the actual implementation of all solutions handed in by his/her group.
Students and coordinators meet once per week for a two-hour lecture in which the coordinators present new exercises and explain the required algorithms and theoretical background. Lecture notes covering the contents of this lecture will be prepared by the organizers during the course and supplied to the students. Students send their solutions by e-mail to algoprak@hpmayr1.informatik.tu-muenchen.de. Comments on their solutions and grading information are sent to the students by e-mail by their respective supervisors as well. Problems encountered by the students can be discussed and questions can be answered either during the lecture or with their supervisors.
Programs handed in by the students will be graded according to the following criteria:
In order to get a course certificate, the following criteria must be satisfied:
IMPORTANT: The practical "Design of Algorithms" belongs to Computer Science I according to old regulations, and to Computer Science III according to new regulations (valid from November 1996). Students who must take their final exams (DHP) according to new regulations can NOT use the course certificate for Computer Science I. Students who have the possibility to choose between old and new regulations can use the course certificate for either Computer Science I or Computer Science III. Click here for details (in German)!
|
|
Turau. Algorithmische Graphentheorie. Addison Wesley, 1996 |
|
|
Gibbons. Algorithmic Graph Theory. Cambridge University Press, 1985 |
|
|
Mehlhorn. Data Structures and algorithms 2: Graph algorithms and NP-Completeness, Springer-Verlag, 1984 |
|
|
Papadimitriou, Steiglitz. Combinatorial Optimization: Algorithms and complexity. Prentice-Hall, 1982 |
|
|
Sedgewick. Algorithms. Addison-Wesley, 1988 |
|
|
Tarjan. Data Structures and Network Algorithms. SIAM, 1983 |
|
|
Reingold, Nievergelt, Deo. Combinatorial Algorithms. Prentice-Hall, 1977 |
|
|
Ahuja, Magnanti, Orlin. Network Flows: Theory, Algorithms, and Applications. Prentice Hall, 1993. |