LEA TU München, Institut für Informatik
Lehrstuhl für Effiziente Algorithmen 		DFG Logo

Stand der Forschung und eigene Vorarbeiten

  1. Stand der Forschung
    1. Große reale Netzwerke
    2. Darstellung von Graphdaten
    3. Algorithmische Aspekte
  2. Eigene Vorarbeiten
    1. Entwicklung von Visualisierungstechniken
    2. Erste Schritte bezüglich interessanter Fragestellungen

Stand der Forschung

Die Visualisierung von vernetzten Datensätzen in Form von Graphen ist ein häufig eingesetztes Mittel, um Eigenschaften und Zusammenhänge der Daten zu analysieren und aufzuzeigen. Die Grundlagen für derartige Untersuchungen liegen einerseits in der Information über die darzustellenden Netzwerke und andererseits in der Techniken, die eine sinnvolle graphische Repräsentation der Netzwerke ermöglichen. In beiden Bereichen wurden gerade auch für große Netzwerke bereits viele Analysen, Techniken und Algorithmen entwickelt, die im Folgenden kurz vorgestellt werden sollen. Die Begriffe Netzwerke und Graphen werden dabei weitestgehend synonym verwendet.

Große reale Netzwerke

Bei der Visualisierung großer realer Netzwerke können die Graphen in zwei Gruppen aufgeteilt werden: Einerseits in Graphen, die eine bekannte Struktur eines Netzwerks widerspiegeln. Andererseits sind häufig Netzwerke zu visualisieren, über die keine genauen strukturellen Aussagen vorliegen, wie z.B. das soziale Gefüge in einer Bevölkerungsgruppe oder Referenzen im Internet. Gerade wegen dieser Beispiele sind die Netzwerke des zweiten Typs bis heute Bestandteil zahlreicher wissenschaftlicher Untersuchungen.
Netzwerke mit bekannter Struktur
Netzwerkdaten aus diesem Bereich dienen der Beschreibung funktioneller Strukturen, wie beispielsweise (bio)chemischer Prozesse. So kann der aus der Chemie bekannte Zitronesäurezyklus so durch ein Netzwerk dargestellt werden, dass einzelne Ablaufphasen oder funktionelle Einheiten als Komponenten bzw. Teilgraphen repräsentiert werden. Diese Einheiten können ihrerseits auch wieder unterteilt sein. Auf diese Art und Weise können die Abläufe derart verfeinert werden, dass abschließend ein Netzwerk entsteht, aus dem sowohl die Informationen über die wesentlichen Teilgruppen als auch Details auf der Molekülebene in den involvierten chemischen Reaktionen abgelesen werden können. Die Zusammenhänge im Bereich der Genanalyse und Evolutionstheorie sind andere Beispiele für solche Graphen.
Ferner kann man auf Netzwerke betrachten, die gewissen logischen Strukturen genügen und entsprechend aufgebaut sind. Ein typischer Vertreter dieser Modelle ist die Baumstruktur, wie sie in Organigrammen oder auch in Entscheidungsmodellen vorkommt. Aber auch andere, zum Teil geometrische Einheiten wie Kreise oder Sterne kommen häufig zum Einsatz. Speziell im Bereich der Rechnernetze und Schaltkreise werden diese Modelle als Bausteine zur Konstruktion komplexer Gesamtgebilde verwendet.
Für diese Arten von Netzwerken ist eine Zerteilung für eine hierarchische Darstellung bereits durch den Aufbau vorgeben. Für diese stellt sich daher hauptsächlich die Frage nach einer übersichtlichen Darstellung.
Netzwerke mit unbekannten Strukturen
Für Netzwerke, über die man keine genauen strukturellen Informationen besitzt, gibt es zahlreiche alltägliche Beispiele, wie Zugverbindungen innerhalb eines nationalen Eisenbahnnetzes, Darstellungen von Bekanntschaftsverhältnissen zwischen Personen, etwa Vorgesetztenverhältnisse oder der sogenannte Hollywood-Graph (welcher Schauspieler hat bereits mit welchem in einem gemeinsamen Film gespielt). Eine in letzter Zeit immer häufiger untersuchte Gruppe von Graphen ist die aus dem Bereich des World Wide Web. Hier wurden besonders die physikalischen Netzwerke sowie der Referenz-Graph untersucht.
Konzept der Small World Graphen
Um allgemeine Aussagen über die Graphen machen zu können, wurde versucht, Modelle zu definieren, die grundlegende Eigenschaften dieser Graphen zusammenfassen.
Für eine große Menge von Netzwerken, darunter auch die oben genannten, wurde der Begriff der Small World Graphen geprägt [Wat99]. Es handelt sich dabei um die Graphen, die die folgenden Eigenschaften besitzen: In der Vergangenheit wurden diese Eigenschaften für die oben genannten Netzwerke nachgewiesen. Für die ungerichteten Graphen konnte dies problemlos geschehen [Ada99, AJB99], für gerichtete Netzwerke hingegen müssen einige Definitionen weiter gefasst werden.
Nachdem die Gruppe der Small World Graphen eine adäquate Beschreibung für die betrachtenten Netzwerke zu sein scheint, wurden auch viele Anläufe unternommen, Modelle zu entwickeln, die den Anforderungen der Small World Graphen genügen. Im Folgenden sind einige ungerichtete Modelle für Small World Graphen aufgelistet:
Durchgeführte Analysen für die Referenzstruktur des WWW
Gerade für das die Referenzstruktur im WWW wurden zahlreiche Untersuchungen durchgeführt. Den Untersuchungen wurden hierbei zwei verschiedene Datenmodelle zugrunde gelegt. Neben dem ungerichteten Graphen, in dem eine Kante für eine Referenz zwischen zwei Webseiten steht, wird gerade in den letzte Jahren immer häufiger der kompliziertere gerichtete Fall untersucht.
Im Wesentlichen ergibt sich in beiden Fällen eine große Zusammenhangskomponente, die ca. 90% der Knoten enthält. Für den ungerichteten Fall hat diese die Struktur eines dichten Graphen, der sich an seinen Rändern immer mehr verästelt.
Im gerichteten Fall, für den auch die Bezeichnung Web-Graph geprägt wurde, ergaben jüngste Untersuchungen [BKM+00], dass sich die große Zusammenhangskomponente in vier ungefähr gleichgroße Teile unterteilen lässt. Dies Komponenten sind: eine starke Zusammenhangskomponente (SCC), eine Menge von Knoten (IN) von denen aus die Menge SCC erreicht werden kann, jedoch nicht umgekehrt, eine Menge von Knoten (OUT), die von der Menge SCC erreichbar ist, jedoch wiederum nicht umgekehrt. Bei den restlichen Knoten (Tendrils und Tubes) handelt es sich um die Knoten, die die Menge SCC weder erreichen noch von dieser erreichbar sind (siehe Abbildung).
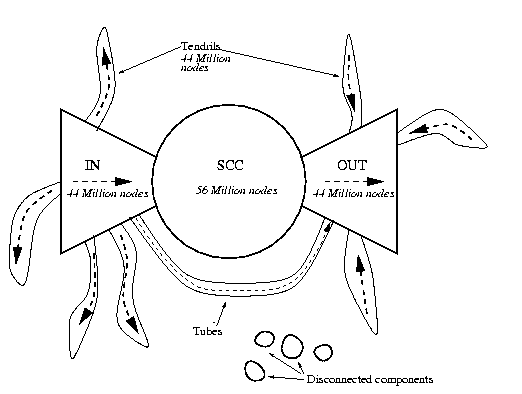Web Graph für WWW Referenzen [BKM+00]

Sowohl für den gerichteten als auch den ungerichteten Fall wurden in zahlreichen Analysen folgende Eigenschaften festgestellt:

Zusammenfassung und weitere Fragestellungen
Die Untersuchungen belegen somit, dass große reale Graphen, soweit sie nicht nach einem strukturellen Prinzip aufgebaut sind, häufig in die Menge der Small World Graphen eingeordnet werden können.
Es sind erste Schritte unternommen worden, um strukturelle Eigenschaften der Graphen sowie einige Modelle zu untersuchen. Gerade das power-law Modell scheint speziell für das World Wide Web eine gute Beschreibung zu sein. Es wurden bereits einige Algorithmen, z.B. für kürzeste Pfade oder Suche im WWW [Kle00, BP98], entwickelt, die auf derartigen Untersuchungen basieren.
Es bleibt jedoch anzumerken, dass noch viele Fragestellungen diesbezüglich offen, oder nur unter zusätzlichen Annahmen über die Graphtopologie gelöst sind.

Darstellung von Graphdaten

Schon seit langem wird an Methoden und Heuristiken gearbeitet, die eine gute Darstellung von Graphen auf dem Bildschirm ermöglichen. Gerade in den letzten Jahren wurde neben reinen Darstellungstechniken das Problem der Darstellung von großen Datenmengen, so beispielsweise von Graphen mit einigen tausend Knoten relevant. Gängige Lösungsansätze für diese Aufgabe werden abschließend zusammengefaßt.
Allgemeine Aspekte
Die bildliche Darstellung eines Graphen soll im wesentlichen dazu dienen, Information über die Graphdaten möglichst übersichtlich und kompakt zu repräsentieren. Dies beinhaltet neben dem reinen Zeichnen, d.h. Anzeigen von Knoten und Kanten, auch eine sinnvolle Umsetzung von weiteren Graphinformationen durch Beschriftung bzw. geeigneter Visualisierung von Kanten/Knoten. Diese Zusatzinformationen müssen so in die Darstellung eingearbeitet werden, dass sie zur weiteren Informationsgewinnung herangezogen werden können.
Ferner sollen die Elemente des Graphen so angeordnet werden, dass Abhängigkeiten von Komponenten oder Teilgraphen ersichtlich sind. Hierzu zählen auch identische Darstellungsformen aller isomorpher Subgraphen. Erst eine solche Darstellung ermöglicht es, die zugrundeliegende Struktur eines Graphen schnell zu erfassen.
Um diese Ziele umzusetzen, kann man einige Methoden für eine gute Darstellung formulieren. Hierunter fallen beispielsweise das Kräftemodell, die Planarisierung von Graphen oder die Orthogonaldarstellung. Neben diesen Anforderungen werden jedoch zumeist auch ästhetische und strukturelle Ziele verfolgt, um dem Betrachter ein möglichst übersichtliches Bild zu liefern [DC98]. Einige dieser Ziele wie Kreuzungsminimierung, sinnvolle Platzausnutzung oder gleichlange Kanten sind bereits teilweise in den erwähnten Techniken integriert.
Es bleibt jedoch anzumerken, dass sich einige der Qualitätskriterien widersprechen. In solchen Fällen sind je nach Zielsetzung der Visualisierung die konkurrierenden Kriterien zu gewichten. Eine ausführliche Beschreibung von gängigen Visualisierungstechniken ist in [DETT98] zu finden.
Darstellung großer Graphen
Werden die zu zeichnenden Graphen groß, d.h. einige tausend Knoten und mehr, so stößt man mit herkömmlichen Methoden schnell an die Grenzen des Machbaren. Würde man alle Informationen darstellen, so entstünde ein unüberblickbares und damit unbrauchbares Bild. Es sind also neue Wege notwendig, um diese Datenflut zu bewältigen.
Ein erster Ansatz ist, die übliche 2-dimensionale Darstellung um eine Dimension zu erweitern. Dies kann einen besseren Eindruck für den Graphen liefern, wenn der Graph von verschiedenen Blickwinkeln betrachtet werden kann. Man muss jedoch berücksichtigen, dass für eine entsprechende Visualisierung meist wieder eine Projektion in die Ebene nötig wird.
Eine andere Möglichkeit besteht in der Beschränkung auf einen so Ausschnitt des Graphen, den man leicht darstellen kann. Diesen Ausschnitt kann man dann über den Graphen wandern lassen, um so alle Teilbereiche betrachten zu können. Diese Lösung ist problematisch, da eine Gesamtansicht des Graphen fehlt. Durch sphärische Transformationen, mit denen man am Rand des aktuellen Teilbereichs den restlichen Graphen verzerrt darstellt, kann man dies umgehen. Dies Methode wird als Fisheye-View bezeichnet.
Ein anderer Ansatz simuliert ein physikalisches Modell. D.h. wenn man einen großen Graphen betrachten möchte, muss man dies aus ausreichender Entfernung tun. In diesem Fall sieht man jedoch nicht alle Details sondern nur einige Merkmale. Geht man näher an den Graphen heran, verschwinden einige Bereiche aus dem Blickwinkel, dafür kommen mehr Detail-Informationen zum Vorschein. Dies kommt einem Zoom auf den Graphen gleich. Wichtig bei dieser Vorgehensweise ist die sogenannte mental map. Darunter versteht man das Bild, das sich ein Betrachter vom Graphen macht. Dieses Bild soll auch bei häufigen Betrachtungswechseln stimmig bleiben. Wenn man auf einen Teilbereich zoomt und dann den Fokus wieder vergrößert, soll sich wieder das gleiche Bild ergeben wie vor dem Zoomen. Gleiches gilt beim Wandern über den Graphen.
Bei diesen Möglichkeiten mit großen Datenmengen zu arbeiten, erkennt man schnell den wesentlichen Kern des Problems. Es ist nicht möglich, alle Daten anzuzeigen, sondern man muss einen Graphen repräsentieren, der einen "gewünschten" Teil der Informationen darstellt. Die allgemein als sinnvoll betrachteten Ansätze zerfallen in zwei Kategorien: die Selektion und die Abstraktion.
Die Selektion arbeitet nach dem Prinzip, aus einer großen Datenmenge lediglich einzelne Teile herauszufiltern und nur diese anzuzeigen. D.h. alle Daten, die einem gewissen Kriterium nicht genügen (z.B. Knotengrad, Kantengewicht etc.), werden nicht betrachtet. Der resultierende Graph ist also ein Teilgraph des ursprünglichen Graphen.
Bei der Abstraktion hingegen werden alle Daten in den Prozess einbezogen. Resultat ist ein neuer Graph. Für die Repräsentation der Ergebnisses des Prozesses durch einen Graphen gibt es verschiedene Möglichkeiten. Eine sehr häufig eingesetzte Methode ist die der Partitionierung. Dafür wird der Graph so in Teile zerlegt, dass diese bezüglich eine bestimmte Bewertungsfunktion optimal gewählt sind. Die einzelnen Teile werden dann als Knoten im neuen Graph verwendet. Für eine ausführlichere Beschreibung zum Thema Partitionierung siehe [Algorithmische Aspekte]. Ist man jedoch nicht nur an einer einzigen Abstraktionsstufe interessiert bzw. reicht diese nicht aus, so kann man das Verfahren auch rekursiv anwenden und kommt so zu einer hierarchischen Repräsentation. Auf jeder Ebene steht ein Graph, dessen Knoten wiederum für andere Graphen stehen, bis auf unterster Ebene einzelne Teilgraphen des Ausgangsgraphen stehen, aus denen der gesamte Graph zusammengesetzt werden kann. Dieses Prinzip ist in folgender Abbildung dargestellt (linke Seite 2-dimensional, rechte Seite 3-dimensional).
Beispiel für eine hierarchische Zerteilung eines Graphen

Mit dieser hierarchischen Zergliederung eines Graphen gibt es nun neue Möglichkeiten, die Graphdaten zu repräsentieren. Der Benutzer kann nun ausgehend von der gröbsten Abstraktion einen Teil des Graphen immer genauer betrachten (vertikales Navigieren). Ferner ist es auch möglich, auf einer Ebene zwischen Abstraktionen für verschiedene Teilausschnitte zu wechseln (horizontales Navigieren).

Zusammenfassung und weitere Fragestellungen
Für die Darstellung von großen Netzwerken existieren zahlreiche Methoden zur Visualisierung. Dabei erweist sich der Ansatz einer hierarchischen Aufteilung des Graphen als sehr sinnvoll. Für diese Art der Darstellung sind einige Präsentationsalgorithmen entwickelt worden, siehe beispielsweise [Ee96]. Hierbei werden zumeist die Darstellungen für einen gegebenen Graphen berechnet und dann dem Betrachter in geeigneter Form präsentiert. Für eine Dynamisierung dieses Prozesses wurde bisher noch keine geeignete Lösung gefunden, die ein wiederholtes Berechnen der kompletten Aufteilung vermeidet. Es fehlen also noch Erkenntnisse, wie sich ein Änderung des Graphen auf die Partitionierung auswirken.

Algorithmische Aspekte

Im Rest dieses Teilabschnitts werden nun einige Fragestellungen und Ergebnisse zu weiter oben nur kurz angesprochenen Problemen und Algorithmen ausgeführt.
Eigenschaften von Graphklassen
Grapheigenschaften können das Ergebnis bzw. die Komplexität eines Algorithmus entscheidend beeinflussen. Wie bereits gesehen, ist es aber nicht immer möglich, diese Aussagen für einen Graphen vorab zu treffen. Häufig greift man deshalb auf Modelle oder Graphklassen zurück. Hierfür werden dann wesentlichen Eigenschaften erforscht und möglichst genau eingegrenzt. Zwei wichtige Gruppen von Eigenschaften mit entsprechenden Anwendungen seinen nur exemplarisch genannt:
Partitionieren
Im Bereich der Partitionierung, d.h. Aufteilung von Graphen, wurde bereits viel Vorarbeit geleistet. Gerade im VLSI-Design sind mehrere Methoden entwickelt worden [Len90]. Grundlegend bei der Partitionierung ist die Bewertungsfunktion. Als Parameter stehen dabei strukturelle Daten der Graphen (Knotengrade, Kanten- und Knotenanzahlen etc.) sowie Bewertungen von Kanten und Knoten zur Verfügung.
Zu den einfachsten Bewertungsfunktionen zählt die des Min-Cut, der zählt, wieviel Kanten über den Schnitt gehen, bzw. wie groß die Summe der entsprechenden Kantengewichte ist. Meist ist es jedoch sinnvoll, die Forderungen nicht nur an die Größe des Schnitts zu stellen, sondern auch die Größe der Komponenten zu berücksichtigen. Neben der klassischen Forderung, dass die Komponenten gleich groß sein sollen, kann man auch Schwankungen zulassen bzw. die Größe der Komponenten mit in die Funktion aufnehmen. Eine häufig verwendete Funktion ist der sogenannte Ratio-Cut [WC91, RS97]. Ab und an stößt man auf leicht unterschiedlich Definitionen, aber im Wesentlichen wird der Quotient aus der Größe des Cuts und dem Produkt der Größen der Komponenten verwendet. Es nehmen also die Partitionen einen kleinen Wert an (es wird in diesem Fall das Minimum gesucht), die einen geringen Cut bei möglichst ausgewogenen Partitionsgrößen besitzen.
Unglücklicherweise führen jedoch diese Bewertungsfunktionen, die auch eine Größenanforderung beinhalten, zu NP-vollständigen Problemen [GJ79]. Jene ohne dies Anforderung gibt es effiziente Algorithmen, deren Lösungen für viele Graphen aufgrund der ungleichen Größenverhältnisse der resultierenden Partitionen jedoch nicht verwertbar sind. Um das Problem dennoch algorithmisch bearbeiten zu können, wurden viele Methoden vorgeschlagen. Einige Ansätze, um gute Partitionierungen erzielen, sind im Folgenden aufgelistet:

Eigene Vorarbeiten

Entwicklung von Visualisierungstechniken

Im Rahmen von Diplomarbeiten wurden bereits Erfahrungen im Bereich Visualisierung von Daten und Algorithmen gesammelt. Ein Schwerpunkt lag hierbei auf der Visualisierung von Graphen und zugehörigen Algorithmen. Hier seien drei Arbeiten exemplarisch genannt:

Erste Schritte bezüglich interessanter Fragestellungen

Als direkte Vorarbeiten zu diesem Projekt sind noch keine Veröffentlichungen erschienen. Es wurden aber bereits erste Untersuchungen gestartet.
Hanjo Täubig
Last modified: Thu Aug 29 13:29:37 CEST 2002