Degree Bounds for Gröbner Bases of Important Classes of Polynomial Ideals and Efficient Algorithms (GBiC PolyA)
Project
Basic Facts about Gröbner Bases
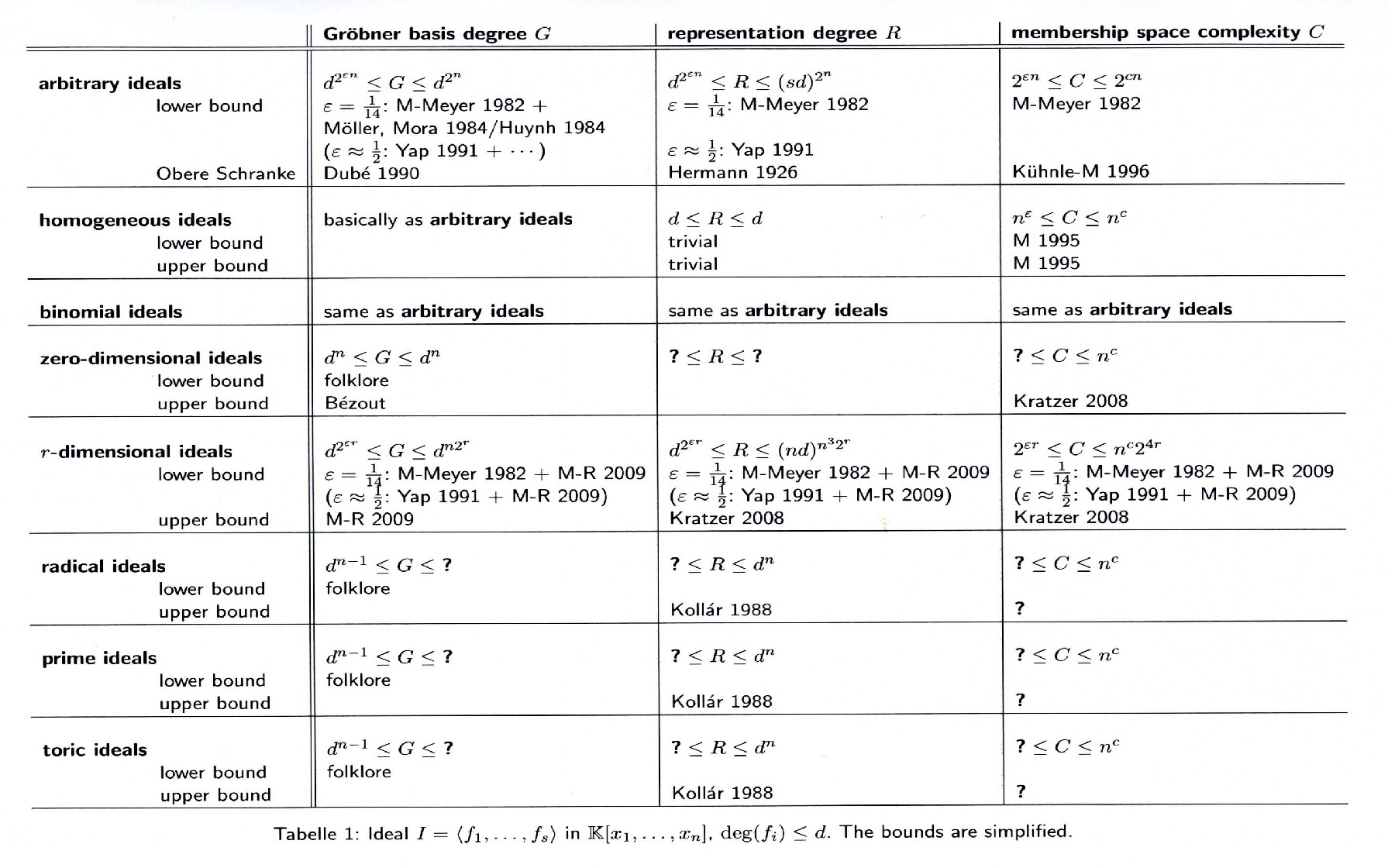
Gröbner bases were introduced by Buchberger in order to solve the ideal membership problem for multivariate polynomials over a field. For a fixed monomial ordering, they provide unique representations of polynomials ideals.However, their computation is extremely hard. Buchberger's algorithm needs double exponential space in the worst case. For arbitrary algorithms computing Gröbner bases and/or solving the ideal membership problem, Mayr and Meyer gave a single exponential space lower bound.
Uses of Gröbner Bases
Being a very general and versatile tool, Gröbner bases are useful in many different areas. There are two major approaches to use them in optimization: one can either use Gröbner bases in order to solve optimality conditions like Karush-Kuhn-Tucker (neglecting inequalities and later verifying solutions) or in order to construct a test set. This approach is used in integer linear programming.Automatic theorem proving is another field of applications for Gröbner bases. The preconditions and the claim have to be formulated as polynomial equations, which is especially easy in geometry. The verification of the claim then reduces to some kind of radical membership test.
Further application fields include algebraic geometry, which is the study of algebraic varieties, motion planning in robotics, and cryptography. In the DFG focal point, project groups PB7 "`Familien von Varietäten"', PB8 "`Desingularisierung"', PB9 "`Torische und tropische Geometrie, Mirrorsymmetrie"', PB12 "`Zertifiziertes Lösen polynomieller Gleichungssysteme mit numerisch-symbolischen Methoden"' und PB13 "`Algebraische Methoden in der Kryptographie"' are involved with Gröbner bases.
Tools for Computing Gröbner Bases
Most modern computer algebra systems provide at least basic algorithms for computing Gröbner bases (e.g. Singular, Macaulay2, Mathematica, Maple). They differ when it comes to efficiency and advanced algorithms. Also specialized software packages are available (e.g. 4ti2 for toric ideals).Proof Techniques
The most elegant technique to prove upper degree bounds for Gröbner bases was introduced by Dubé and adopted by M-R. It exploits the fact that the monomial ideal of leading terms is generated by the elements of a Gröbner basis and geometrically constructs the worst case for a reduced Gröbner basis, the so-called exact cone decompositions. The lower bounds, first by M-Meyer, are actually proven for commutative semigroups and easily transfer to polynomial ideals. They use state variables to realize some kind of counting.One of the fundamental results in this area was given by Hermann. She proved that, if a polynomial equation system is solvable, solutions with bounded degree exist. Today this is referred to as the representation degree. The main idea was to consider some of the variables as elements of the base ring and apply an recursive algorithm. For radical ideals, better bounds have been given, e.g. by Kollár, mostly using analytic reasoning. Lower bounds for this degree can also be derived from M-Meyer.
The complexity results rely on two main techniques which they combine with the degree bounds for Gröbner bases and representation degree. For upper bounds, first done by Kühnle-M, the problem is written as linear equation system which can be solved in logarithmic time (in the size of the system) on a parallel machine. By a well-known theorem, this is equivalent to logarithmic space on a sequential machine. The lower bounds simulate bounded three-counter machines for which space-hardness results exist, a technique introduced by M-Meyer.
Members
- Prof. Dr. Ernst W. Mayr (project leader)
- Stefan Toman
Former Members
Conference Papers
Ernst W. Mayr and Stephan Ritscher: Degree bounds for Gröbner bases of low-dimensional polynomial idealsErnst W. Mayr and Stephan Ritscher: Space-efficient Gröbner basis computation without degree bounds
Students' Theses
Currently Known Complexity Bounds